В предыдущей статье мы узнали о таких показателях, как диапазон вариаций, межквартильный диапазон и среднее линейное отклонение. В этой статье мы изучим дисперсию, стандартное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины является одним из основных показателей в статистике. Он отражает меру разброса данных вокруг среднего арифметического.
Теперь небольшой экскурс в теорию вероятностей, лежащую в основе математической статистики. Как и ожидаемое значение, дисперсия является важной характеристикой случайной величины. Если математическое ожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей:
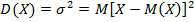
То есть спред – это математическое ожидание отклонений от математического ожидания.
На практике при анализе проб математическое ожидание, как правило, неизвестно. Поэтому вместо этого используется оценка: среднее арифметическое. Дисперсия рассчитывается по формуле:
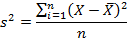
куда
s2 — выборочная дисперсия, рассчитанная по данным наблюдений,
Х — отдельные значения,
X̅ — среднее арифметическое выборки.
Следует отметить, что такой расчет дисперсии имеет недостаток: он необъективен, то есть его математическое ожидание не равно истинному значению дисперсии. Подробнее об этом здесь. Однако с увеличением размера выборки он все еще приближается к своему теоретическому аналогу, то есть является асимптотически несмещенным.
Проще говоря, дисперсия — это средний квадрат отклонений. То есть сначала вычисляется среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, прибавляется, а затем делится на количество значений в этой совокупности. Разница между индивидуальным значением и средним значением отражает меру отклонения. Он возводится в квадрат, чтобы гарантировать, что все отклонения преобразуются исключительно в положительные числа, и чтобы положительные и отрицательные отклонения не компенсировали друг друга при сложении. Затем, имея квадраты отклонений, просто вычисляем среднее арифметическое. Среднеквадратичное отклонение. Отклонения возводят в квадрат и считают среднее значение. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
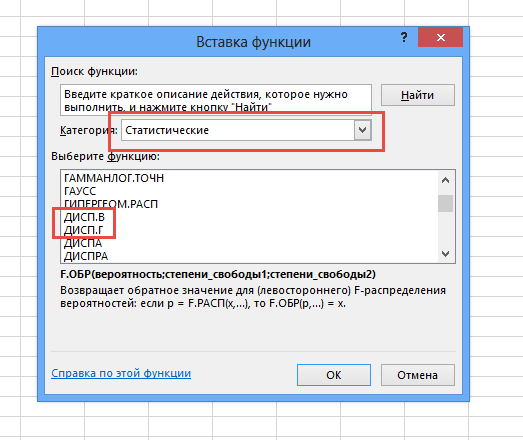
Общие и выборочные отклонения легко рассчитать в Excel. Имеются специальные функции: DISP.H и DISP.V соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, при статистической проверке гипотез или вычислении коэффициентов корреляции. Поэтому было бы неплохо знать математические свойства рассеяния.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины А равна 0 (нулю).
Д(А) = 0
Свойство 2. Если случайную величину умножить на константу А, то дисперсия этой случайной величины увеличится в А2 раза. Другими словами, постоянный множитель можно вывести из-под знака рассеяния, возведя его в квадрат.
D(AX) = A2D(X)
Свойство 3. Если мы прибавим (или вычтем) константу А к случайной величине, то дисперсия останется неизменной.
Д (А + Х) = Д (Х)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
Д(Х+У) = Д(Х) + Д(У)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разности также равна сумме дисперсий.
Д(ХУ) = Д(Х) + Д(У)
Среднеквадратичное (стандартное) отклонение
Если вы возьмете квадратный корень из дисперсии, вы получите среднеквадратичное (стандартное) отклонение корня (сокращенно RMS). Есть название стандартного отклонения и сигмы (от названия греческой буквы). Общая формула стандартного отклонения в математике выглядит следующим образом:
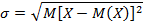
На практике формула стандартного отклонения выглядит следующим образом:
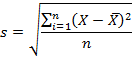
Как и в случае с дисперсией, тут немного другой вариант расчета. Но по мере роста образца разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Чтобы вычислить стандартное отклонение, просто возьмите квадратный корень из дисперсии. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (для генеральной и выборочной совокупности соответственно).
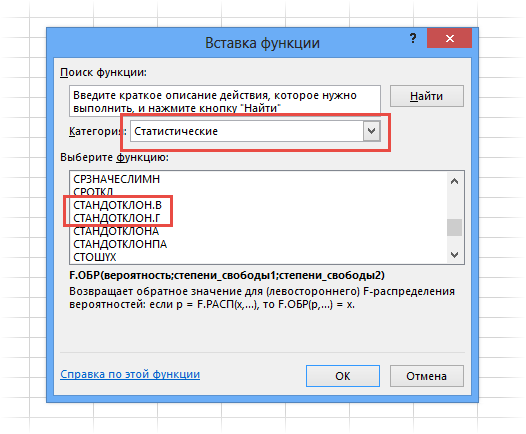
Стандартное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому оно сопоставимо с исходными данными.
Коэффициент вариации
Величина стандартного отклонения зависит от масштаба самих данных, что делает невозможным сравнение изменчивости разных выборок. Для устранения эффекта масштаба необходимо рассчитать коэффициент вариации по формуле:
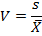
Его можно использовать для сравнения однородности явлений даже при разных масштабах данных. В статистике принято, что если значение коэффициента вариации меньше 33 %, то совокупность считается однородной, если больше 33 %, то неоднородной. Собственно, если коэффициент вариации превышает 33%, то ничего особенного с этим делать не нужно. Это общая информация. Как правило, коэффициент вариации используется для оценки относительной дисперсии данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится путем деления стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.B()/СРЕДНЕЕ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейку формулы можно отформатировать в процентах:
Коэффициент осцилляции
Еще одним показателем разброса данных на сегодняшний день является коэффициент осцилляции. Это отношение размаха вариаций (разницы между максимальным и минимальным значениями) к среднему значению. Готовой формулы Excel не существует, поэтому вам нужно объединить три функции: MAX, MIN, AVERAGE.
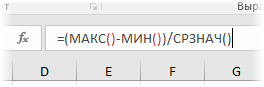
Коэффициент колебания показывает степень отклонения от среднего, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже представлено видео о том, как рассчитать коэффициент вариации, дисперсию, стандартное отклонение (среднеквадратичное) и другие показатели вариации в Excel.
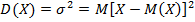

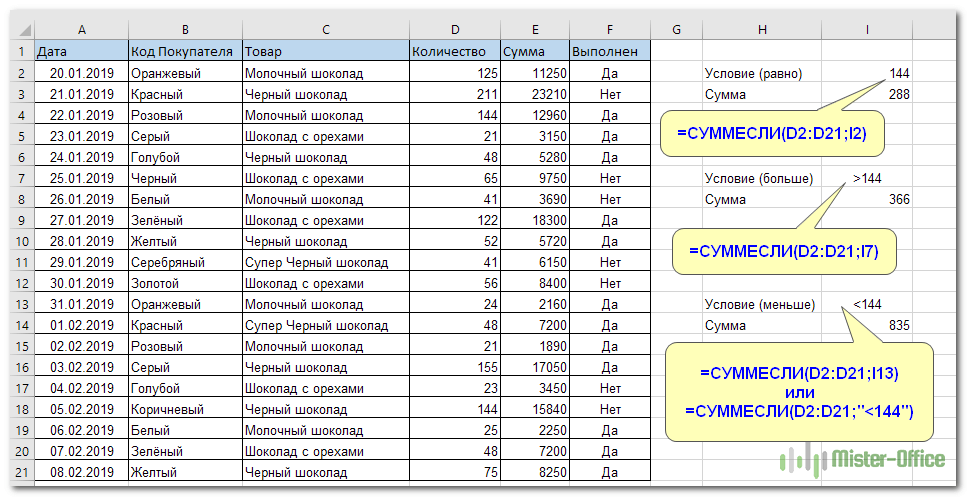



.png)

.png)

.png)

